《模型思维》之幂律分布

幂律分布就是通常所称的长尾分布或重尾分布。在把这种分布绘制在图上时，会产生对应大事件的沿水平轴运行的长尾。例如城市人口分布、物种灭绝、万维网上的链接数量以及企业规模等，所有这些分布都有很长的尾巴，视频下载量、书籍销量、学术论文引用数量、战争中的伤亡人数、洪水和地震的分布也是如此。

产生幂律分布要求非独立性，通常以正反馈的形式出现。社会学家罗伯特·默顿（RobertMerton）把这种已经拥有更多的人未来也能够得到更多的现象称为马太效应（Matthew effect），正如《圣经》中所说：“凡有的，还要加给他，叫他有余；凡没有的，连他所有的，也要夺去。”（马太福音25:29）

既然在各种领域中都能发现发幂律分布，那么如果有某个机制可以解释所有这些幂律分布就太好了，可惜的是，这种机制并不存在。

一、幂律分布的结构

一个定义在区间［xmin，∞）上幂律分布可以写成如下形式：

P(x)=Cx-a

其中，指数a＞1决定了尾部的长度，同时常数项

确保总概率的分布。幂律中指数的大小决定了大事件的可能性和大小。当指数等于2时，事件的概率与其大小的平方成比例。

大事件的可能性将幂律分布与正态分布区分开来，因为在正态分布中，我们实际上从未见过大事件，而在幂律分布中，大事件虽然也很少见，但是它们发生的频率足以引起注意和准备。即使是百万分之一的事件也必须加以考虑。

幂律分布有明确的定义，不是每一个长尾分布都是幂律分布。要想快速地检验某个分布是不是幂律分布，可以用双对数坐标系把该分布画出来：双对数坐标系可以将事件大小及其概率转换为相应的对数值，并将幂律分布转换为直线。

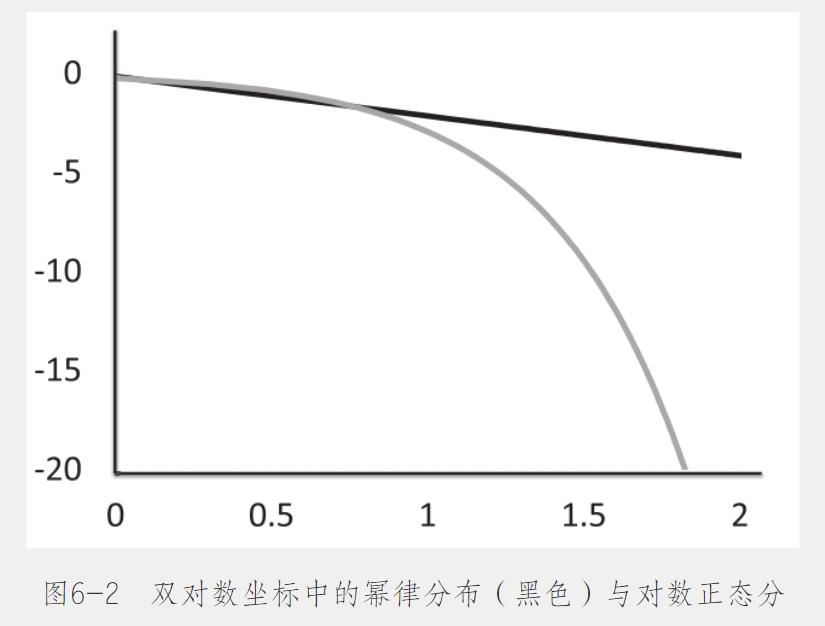
齐普夫分布（Zipf distribution）是幂律分布的一个特例，即指数等于2的幂律分布。即：事件等级×事件大小=常数。

2、优先连接模型

一连串物体（人）一个接一个地到达。第一个到达者创建一个实体。后续每次有人到达时都应用以下规则：在概率p（较小）的情况下，新到达者创造一个新的实体；在概率（1-p）的情况下，新到达者加入现有的某个实体。加入某个特定实体的概率等于该实体的大小除以到目前为止所有到达者的数量。

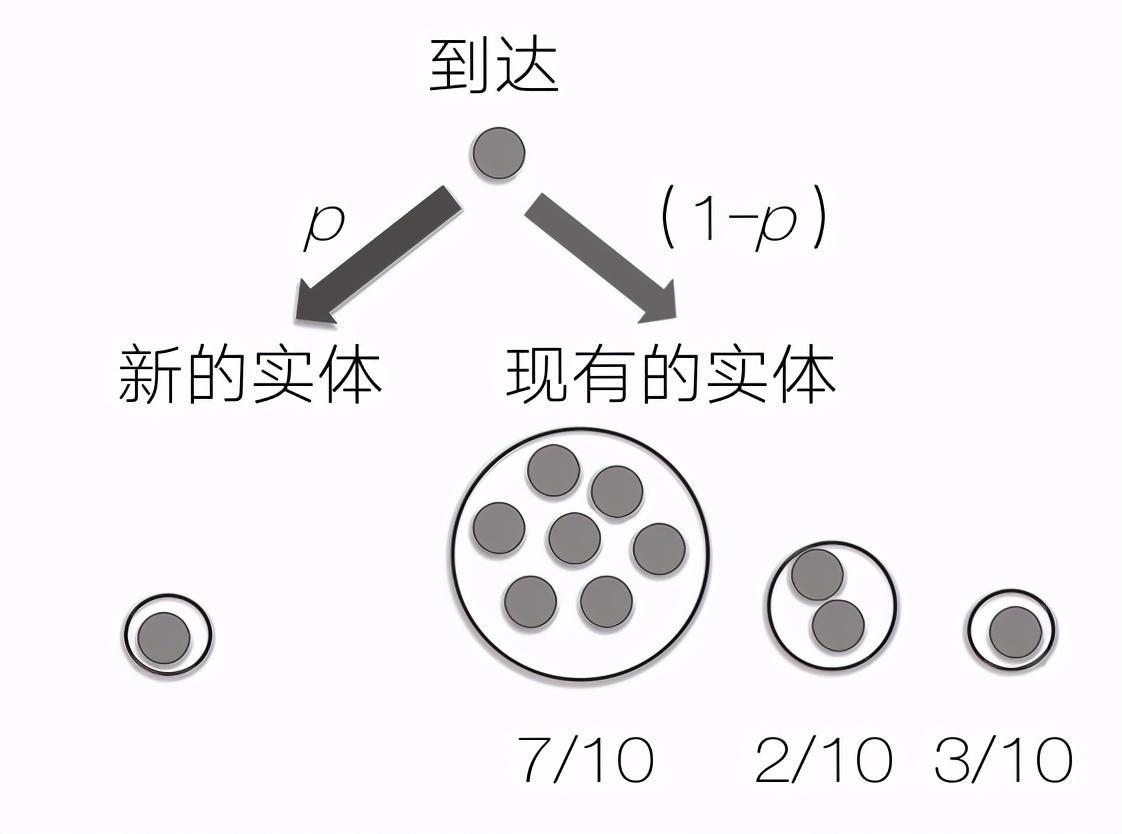
优先连接模型有助于解释为什么网络链接、城市规模、企业规模、图书销量和学术引用数量的分布都是幂律分布。在这些情况下，一个行动（比如一个人购买了一本书）会增加其他人也这样做的可能性。如果从某家企业购买商品的概率与它在当前市场的份额成正比，同时如果新企业进入市场的概率较低，那么优先连接模型预测企业规模的分布将是幂律分布。同样的逻辑也适用于图书销量、音乐下载量和城市发展。

2、自组织临界模型

它通过在系统中建立相互依赖关系的过程产生幂律分布，直到系统达到临界状态为止。自组织临界模型有很多种。

沙堆模型（sand pile model）假设有人将沙粒从距桌面几十厘米的地方洒落到桌子上。随着沙粒不断增多，一个沙堆开始形成。最终，沙子的堆积会达到临界状态，此后每加一次沙子都可能导致“沙崩”。在这种临界状态下，多加入的沙子通常要么没有影响，要么最多只会导致一些沙子下滑。这些属于幂律分布中的数量众多的小事件。但有时，只要再加入一粒沙子就会导致大规模的“沙崩”，这就是大事件。

森林火灾模型（forest fire model）“森林”最初只是一个空的N×N网格。每个周期在网格上随机选择一个格点。如果该格点为空，那么就以概率g在那里种上一棵树。如果该格点上已经有树，那么闪电会以概率（1-g）击中该格点。如果该格点有一棵树，那么树会着火，火势会蔓延到所有连接到该格点的有树的格点。这里需要注意的是，在森林火灾模型中，被闪电击中的概率等于1减去种树的概率。

在沙堆模型和森林火灾模型中，宏观层面的变量，也就是沙堆的高度或森林的密度，都具有一个临界值。当有像沙崩或火灾这样的大事件发生时，宏观层面的变量值会减小。这两个模型的一些变体可以解释太阳耀斑、地震和交通拥堵的分布。不过，当事件发生时，不断增加的宏观层面的变量会减少，这虽然是必要的，但对于自组织临界性来说是不够的。

3、长尾分布

根据定义，与正态分布相比，长尾分布意味着少数几个大“赢家”（大崩溃、大地震、大火灾和严重的交通拥堵）和很多的“输家”；而正态分布则是关于均值对称的。长尾分布也可能增加波动性，因为更大实体中的随机波动会产生更大的影响。

对公平的含义：尾巴变长了，社会影响增加了不平等。大赢家的出现不是随机的，但它们其实并不一定是最好的。

对灾难的含义：森林火灾模型能够让我们意识到临界密度的存在。临界密度可能因森林而异，可能取决于树木的类型、盛行风速和地形。这个模型有效地解释了为什么森林会出现自组织临界状态。比如银行是不是和森林一样呢？

对波动性的含义：如果组成幂律分布的实体规模出现了波动，那么幂律的指数就可以作为衡量系统层面波动性的一个代表。由此可以推断，企业规模的分布应该会影响市场波动性。例如，我们可以将某个国家的国内生产总值视为数千家企业的总产量。如果各家企业的生产水平相互独立且变差有限，那么根据中心极限定理，这个国家的国内生产总值分布将服从正态分布。也就是说，企业生产水平的差异越大，总体波动性就越大。如果企业规模的长尾分布导致生产水平上更大的变差，那么这种长尾分布也必定与更大的总体波动性相关。

4、设想长尾分布的世界

长尾分布是由于反馈和相互依赖性而产生的。我们应该高度注意这个结果。随着世界中相互联系性的提高和反馈的增加，我们应该会观察到更多的长尾分布，同时现在关注的这些长尾分布的尾部也可能会进一步拉长。这就是说，不平等可能会增加，灾难可能变得更大，波动性也会变得更加剧烈。

机会的增加可以创造风险激励，这个逻辑可以应用到很多领域。风险资本家经常冒险，因为他们有机会进行多项投资。